Polytope model

The polyhedral model (also called the polytope method) is a mathematical framework for loop nest optimization in program optimization. The polytope method treats each loop iteration within nested loops as lattice points inside mathematical objects called polytopes, performs affine transformations or more general non-affine transformations such as tiling on the polytopes, and then converts the transformed polytopes into equivalent, but optimized (depending on targeted optimization goal), loop nests through polyhedra scanning.

Detailed example

The following C code implements a form of error-distribution dithering similar to Floyd–Steinberg dithering, but modified for pedagogical reasons. The two-dimensional array src contains h rows of w pixels, each pixel having a grayscale value between 0 and 255 inclusive. After the routine has finished, the output array dst will contain only pixels with value 0 or value 255. During the computation, each pixel's dithering error is collected by adding it back into the src array. (Notice that src and dst are both read and written during the computation; src is not read-only, and dst is not write-only.)

Each iteration of the inner loop modifies the values in src[i][j] based on the values of src[i-1][j], src[i][j-1], and src[i+1][j-1]. (The same dependencies apply to dst[i][j]. For the purposes of loop skewing, we can think of src[i][j] and dst[i][j] as the same element.) We can illustrate the dependencies of src[i][j] graphically, as in the diagram on the right.

 #define ERR(x,y) (dst[x][y] - src[x][y])
 
 void dither(unsigned char **src, unsigned char **dst, int w, int h)  
 {
     int i, j;
     for (j = 0; j < h; ++j) {
         for (i = 0; i < w; ++i) {
             int v = src[i][j];
             if (i > 0)
               v -= ERR(i - 1, j) /2;
             if (j > 0)
               v -= ERR(i, j - 1) / 4;
             if (j > 0 && i < w - 1)
               v -= ERR(i + 1, j - 1) / 4;
             dst[i][j] = (v < 128) ? 0 : 255;
             src[i][j] = (v < 0) ? 0 : (v < 255) ? v : 255;
         }
     }
 }

Performing the affine transformation 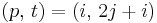on the original dependency diagram gives us a new diagram, which is shown in the next image. We can then rewrite the code to loop on p and t instead of i and j, obtaining the following "skewed" routine.

 void dither_skewed(unsigned char **src, unsigned char **dst, int w, int h)  
 {
     int t, p;
     for (t = 0; t < (w + (2 * h)); ++t) {
         int pmin = max(t % 2, t - (2 * h) + 2);
         int pmax = min(t, w - 1);
         for (p = pmin; p <= pmax; p += 2) {
             int i = p;
             int j = (t - p) / 2;
             int v = src[i][j];
             if (i > 0)
               v -= ERR(i - 1, j) / 2;
             if (j > 0)
               v -= ERR(i, j - 1) / 4;
             if (j > 0 && i < w - 1)
               v -= ERR(i + 1, j - 1) / 4;
             dst[i][j] = (v < 128) ? 0 : 255;
             src[i][j] = (v < 0) ? 0 : (v < 255) ? v : 255;
         }
     }
 }

See also

• Frameworks supporting the polyhedral model
• Loop nest optimization
• Loop unrolling
• Loop reversal
• Loop tiling

External links and references

• "The basic polytope method", tutorial by Martin Griebl containing diagrams of the pseudocode example above
• "Framework for polyhedral model"
• "Code Generation in the Polytope Model" (1998). Martin Griebl, Christian Lengauer, and Sabine Wetzel
• "The CLooG Polyhedral Code Generator"
• "CodeGen+: Z-polyhedra scanning"